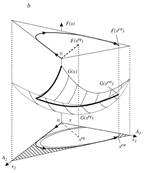
Термодинамически допустимые пути неравновесных процессов:

Пространство путей, Термодинамический анализ динамики, Экстремальные модели промежуточных состояний, Равновесия и кинетика, обход равновесия и всякая всячина…

Можно ли обойти равновесие?

А.Н. Горбань ag153@le.ac.uk, Г.С. Яблонский gy@seas.wustl.edu

Что не запрещено, то разрешено. Так что же запрещено в ходе химических реакций, теплопереноса и других диссипативных процессов? Можно ли «перебросить» систему через равновесие, и если да, то на какую величину? На примере эффектов обхода равновесия обсуждаются термодинамически разрешенные и запрещенные пути процессов. Далее (html); Открыть/скачать PDF-файл

Is It Possible to Circumvent Equilibrium?

A.N. Gorban ag153@le.ac.uk, G.S. Yablonskii gy@seas.wustl.edu

Everything that is not prohibited is permissible. So, what is prohibited in the course of chemical reactions, heat transfer and other dissipative processes? Is it possible to “overshoot” the equilibrium, and if yes, then how far? Thermodynamically allowed and prohibited trajectories of processes are discussed by the example of effects of equilibrium encircling …. html PDF

Горбань А. Н., Яблонский Г. С., Математик - химик: взаимодействие и конфликты, Химия и жизнь, 1987, № 12, 23-27. GorbanYablonskyChemZhizn23_27_12_1987.djvu

Проанализирован многолетний опыт успешного взаимодействия химиков и математиков в совместных исследованиях. Предложена типология конфликтов и путей их разрешения. Обсуждаются различные способы организации совместной работы на стыке наук.

Gorban A.N. Invariant sets for kinetic equations, React. Kinet. Catal. Lett., Vol. 10, No. 2 (1979), 187-190. PDF (or RKCL1978.pdf)
Positively invariant sets in the space of compositions are considered for a closed system, where a complex chemical reaction of a known mechanism proceeds. If the vector of concentrations belongs to such a set at a certain moment of time, it will remain within it at any succeeding moment. Some possible applications are discussed. These positively invariant sets are strongly dependent on the detailed reaction mechanism. This may be used for discrimination of various mechanisms under consideration.

Горбань А.Н. Инвариантные множества для кинетических уравнений. Для закрытых химических систем конструируются положительно инвариантные подмножества пространства составов: если вектор концентраций принадлежит такому множеству в начальный момент времени, то он останется там и в ходе эволюции системы. Обсуждаются некоторые возможные приложения. Рассматриваемые инвариантные множества существенно зависят от механизма реакции. Они могут использоваться в решении задачи дискриминации различных механизмов реакции. PDF (или RKCL1978.pdf )

А.Н. Горбань, Обход равновесия (уравнения химической кинетики и их термодинамический анализ).– Новосибирск: Наука, 1984. – 226 с. [A.N. Gorban. Equilibrium Encircling (Chemical Kinetics Equations and their Thermodynamic Analysis), Nauka, Novosibirsk, USSR, 1984]

Главная тема книги – термодинамический анализ уравнений химической кинетики. Решается вопрос: что можно сказать о динамике химической системы, если известны ее термодинамические функции? Это является частичной реализацией программы ПОследовательного Качественного Анализа уравнений кинетики (ПОКА), предложенной автором. Основная идея ПОКА: исходный материал для построения кинетических моделей состоит из разнородных сведений, как правило, различной степени достоверности и следцует выявить, какие ограничения на динамику накладывают различные составляющие исходной информации. Вот эти составляющие:

А) Список веществ;

Б) Термодинамические функции;

В) Механизм реакции (список элементарных реакций);

Г) Кинетический закон (например, закон действия масс);

Д) Константы скорости.

Этап А дает балансный многогранник, этап Б отделяет термодинамически разрешенные направления от термодинамически запрещенных, на этапе В конус возможных направлений сужается до тех, которые могут быть построены в рамках данного механизма. Если добавить надежное знание о Г и Д, то можно получить кинетические уравнения. Но что делать, если этого знания нет, или, как это часто бывает, знание о списке веществ и термодинамических функциях точнее, чем доступная информация о кинетических константах? Оказывается, что уже этапы А.Б, и Г позволяют многое сказать о кинетике без построения детальных кинетических уравнений. В книге рассказано, как это сделать.

Г.С. Яблонский, В.И. Быков, А.Н. Горбань,Кинетические модели каталитических реакций, Новосибирск: Наука (Сиб. отделение), 1983

Книга посвящена кинетическим моделям каталитических реакций. Бурное развитие исследований в этой области (прежде всего в области нестационарного катализа) обусловлено необходимостью понимания свойств системы «реакционная смесь – катализатор». Анализ кинетических зависимостей необходим как для выяснения детального механизма реакции, так и для разработки принципиально новых технологических решений.

В монографии даны элементы стационарной и нестационарной кинетики сложных реакций, в частности гетерогенного катализа. Особое внимание обращено на приложения теории графов и качественной теории дифференциальных уравнений. Впервые в литературе дается систематическое изложение результатов, большей частью оригинальных, позволяющих связывать наблюдаемое в эксперименте сложное динамическое поведение (множественность стационарных состояний, автоколебания скорости реакции) с видом детального механизма.

Книга предназначена для химиков-кинетиков и математиков, интересующихся формальной химической кинетикой. Она может быть полезной также преподавателям вузов физико-химического профиля, аспирантам и студентам соответствующих специальностей.

В частности, впервые в монографической литературе изложены основные термодинамические ограничения на нестационарную кинетику. Читать и скачивать ЗДЕСЬ (PDF файлы по главам)

G.S. Yablonskii, V.I.Bykov, A.N.Gorban, V.I.Elohin,Kinetic Models of Catalytic Reactions, Elsevier, R.G. Compton (Ed.) Series "Comprehensive Chemical Kinetics", Volume 32, 1991.

The book presents “three kinetics”: (a) detailed, oriented to the elucidation of a detailed reaction mechanism according to its kinetic laws; (b) applied, with the aim of obtaining kinetic relationships for the further design of chemical reactors; and (c) mathematical kinetics whose purpose is the analysis of mathematical models for heterogeneous catalytic reactions taking place under steady- or unsteady state conditions

Besides establishing a general theory permitting us to investigate the dependence of kinetic characteristics for complex reactions on the structure of detailed mechanism, the book provides a comprehensive analysis of some concrete typical mechanisms for catalytic reactions, in particular for the oxidation of carbon monoxide on platinum metals. This reaction is a long-standing traditional object of catalysis study, “Mona Lisa” of heterogeneous catalysis. Читать и скачивать здесь (PDF файлы по главам)

Г.С. Яблонский, В.И. Выков, А.Н. Горбань, В.И. Елохин,Кинетические модели каталитических реакций. Эта книга – не перевод книги 1983 г. на английский – она содержит примерно вдвое больше материала, включая модели реальных реакций и сравнение предсказанных критических явлений с экспериментом.

Книга представляет «три кинетики»: (а) детальную, ориентированную на исследование и использование детального механизма реакции; (б) прикладную, цель которой – получение кинетических зависимостей для дальнейшего использования в конструировании химических реакторов и (в) математическую кинетику, задача которой – анализ математических моделей гетерогенно-каталитических реакций, как в стационарных, так и в нестационарных условиях.

Кроме создания общей теории, позволяющей исследовать зависимость кинетики сложной реакции от структуры ее детального механизма, в книге проводится анализ ряда конкретных типовых механизмов каталитических реакций. Это, в частности, реакция окисления СО на металлах платиновой группы. Это – традиционный объект исследований - Мона Лиза гетерогенного катализа. Читать и скачивать здесь (PDF файлы по главам)

A. N. Gorban, B. M. Kaganovich, S. P. Filippov, A. V. Keiko, V. A. Shamansky & I. A. Shirkalin,Thermodynamic Equilibria and Extrema : Analysis of Attainability Regions and Partial Equilibrium, Springer, Berlin Heidelberg New York (2006)

This book discusses mathematical models that are based on the concepts of classical equilibrium thermodynamics. They are intended for the analysis of possible results of diverse natural and production processes. Unlike the traditional models, these allow one to view the achievable set of partial equilibria with regards to constraints on kinetics, energy and mass exchange and to determine states of the studied systems of interest for the researcher. Application of the suggested models in chemical technology, energy and ecology is illustrated in the examples. … Читать английское издание (PDF по главам); Книга “Thermodynamic equilibria and Extrema” одним файлом (1.6M)

Книга посвящена памяти Льва Соломоновича Полака, замечательного человека и ученого.

Б.М. Каганович, А.В. Кейко, В.А. Шаманский, Равновесное термодинамическое моделирование диссипативных макроскопических систем, Институт систем энергетики им. Л.А. Мелентьева СО РАН, 2007, 76 с.

Обосновывается допустимость равновесных термодинамических описаний необратимых процессов. Излагаются новые модификации модели экстремальных промежуточных состояний (МЭПС), содержащие записанные в термодинамической форме (без использования переменной времени) ограничения на необратимую макроскопическую кинетику. Сопоставляются возможности МЭПС и моделей кинетики и неравновесной термодинамики. Эффективность равновесного моделирования иллюстрируется на примерах анализа химических технологий (в том числе образования оксидов азота при сжигании угля) и потокораспределения в гидравлических системах.

… Чтобы четко объяснить возможности равновесных описаний неравновесных необратимых процессов, конечно, нужно предварительно достаточно точно определить понятия равновесности и обратимости, неравновесности и необратимости. Понятно, что их трактовка, как и трактовка других научных понятий, меняются с развитием соответствующих теорий, моделей и методов. … Далее(PDF-файл ~ 1M)

Shinnar R and Feng C. A.,Structure of Complex Catalytic Reactions: Thermodynamic Constraints in Kinetic Modeling and Catalyst Evaluation, Ind. Eng. Chem. Fundam. 1985, 24, 153-170.

The paper examines the thermodynamic constraints on chemical reaction trajectories. It shows how thermodynamic concepts can be used to organize and analyze the results of kinetic studies in complex reaction systems where several reactions can occur simultaneously. It defines rigorous criteria for setting up a set of stoichiometric relations to obtain an empirical kinetic model for the system. This can уbe done without any kinetic calculations by inspecting the measured trajectories in composition space. The paper also defines the concept of coupling between overall ostensible reactions and explains the thermodynamic advantages by using shape-selective catalysts. The concept of thermodynamic constraint is defined, and it is shown that the mechanism of the kinetic reactions has thermodynamic consequences far more restrictive than the Second Law itself. The results should be useful in the modeling of complex reactions systems as well as in the testing and evaluation of new catalysts. PDF ~ 2.5M

Исследуются термодинамические ограничения на кинетику химических реакций. Показано как понятия термодинамики могут использоваться для систематизации и анализа результатов кинетических исследований сложных реакционных систем. Строго выведены критерии правильности построения эмпирической кинетической модели. Они могут быть проверены без кинетических расчетов прямым изучением измеренной траектории в пространстве составов. В работе определяется также понятие сопряжения («каплинга») фиктивных брутто-реакций и объясняются термодинамические выгоды селективного катализа. Определены термодинамические ограничения и продемонстрировано, что механизм химической реакции имеет термодинамические следствия, которые намного более ограничительны, чем Второе Начало термодинамики. Результаты будут полезны для моделирования сложных реакций так же как для тестирования и оценки новых катализаторов. PDF ~ 2.5M

Эта безусловно интересная статья Шиннара и Фенга удивила В.И. Быкова тем, что даже многие иллюстрации в ней поразительно похожи на иллюстрации к ранее опубликованным (в том числе, и на английском) работам А.Н. Горбаня с соавторами, а ссылок на эти работы нету. В этом сходстве легко убедиться, сравнив иллюстрации к этой статье и к статье А.Н. Горбаня и Г.С. Яблонского, открывающей сайт (эти иллюстрации скопированы из «Обхода равновесия», 1984, и во многом повторяют рисунки из более ранних работ). Также, естественно, похожи формулы и теоретические положения. Удивление В.И. Быкова было настолько сильным и устойчивым, что он написал в журнал, журнал письмо опубликовал, а Шиннар, естественно, ответил. Копию этой опубликованной переписки предлагаем:

V. I. Bykov, Comments on “Structure of Complex Catalytic Reactions: Thermodynamic Constraints in Kinetic Modeling and Catalyst Evaluation” and R. Shinnar, Response to Comments on “Structure of Complex Catalytic Reactions: Thermodynamic Constraints in Kinetic Modeling and Catalyst Evaluation”,Ind. Eng. Chem. Res. 1987, 26, 1943-1944. PDF ~ 300K

В следующих статьях Шиннар уже ссылается:

Shinnar R., Thermodynamic analysis in chemical process and reactor design, Chem. Eng. Sci., 43, Iss. 8 (1988), 2303-2318.

Thermodynamic analysis is a very useful tool for the industrial chemist, catalyst chemist, process designer and the chemical reactor designer. It is not only useful for understanding existing processes; if properly used it can offer stimulating insight into the design of new processes and indicate ideas for improvement of old ones. It can also serve as a guide for future research and development in the areas of catalysts, process design and reactor design. … PDF ~ 1.7M

Термодинамический анализ – это очень полезное инструмент для специалистов по химическим технологиям, химии катализа, для разработчиков промышленных процессов и химических реакторов. Он полезен не только для понимания известных процессов, но, при правильном использовании, порождает новые стимулирующие идеи для разработки новых процессов и улучшения старых. Он также может служить проводником в новых исследования и разработках в области катализа, при создании промышленных процессов и конструировании реакторов. … PDF ~ 1.7M

Gorban, A.N.; Gorban, P.A.; Judge, G. Entropy: The Markov Ordering Approach. Entropy 2010, 12, 1145-1193.

The focus of this article is on entropy and Markov processes. We study the properties of functionals which are invariant with respect to monotonic transformations and analyze two invariant “additivity” properties: (i) existence of a monotonic transformation which makes the functional additive with respect to the joining of independent systems and (ii) existence of a monotonic transformation which makes the functional additive with respect to the partitioning of the space of states. All Lyapunov functionals for Markov chains which have properties (i) and (ii) are derived. We describe the most general ordering of the distribution space, with respect to which all continuous-time Markov processes are monotonic (the Markov order). The solution differs significantly from the ordering given by the inequality of entropy growth. For inference, this approach results in a convex compact set of conditionally “most random” distributions. PDF~0.6M

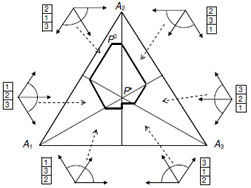
Горбань А.Н., Горбань П.А., Джадж Г. Энтропия: Подход, основанный на Марковском упорядочивании. Entropy 2010, 12, 1145-1193.

Анализируется подход к понятию Энтропии, основанный на Марковских процессах. Изучаются свойства функционалов, которые инвариантны относительно монотонных преобразований. Изучены два инвариантных свойства «аддитивности»: (1) существование монотонного преобразования, которое превращает функционал в аддитивный по отношению к объединению независимых подсистем, и (2) существование монотонного преобразования, которое делает функционал аддитивным по отношению к разбиениям пространства состояний. Определены все функции Ляпунова для Марковских процессов, которые обладают этими свойствами. Описаны наиболее общие порядки на пространстве распределений, по отношению к которым все Марковские процессы монотонны (Марковские порядки). При использовании этого порядка для определения «наиболее случайного» распределения вместо обычных решений, дающих максимум энтропии, появляются выпуклые многогранники «наиболее случайных» распределений. PDF~0.6M

Gorban A.N., Shahzad M., The Michaelis-Menten-Stueckelberg Theorem. Entropy 2011, 13, 966-1019.

We study chemical reactions with complex mechanisms under two assumptions: (i) intermediates are present in small amounts (this is the quasi-steady-state hypothesis or QSS) and (ii) they are in equilibrium relations with substrates (this is the quasiequilibrium hypothesis or QE). Under these assumptions, we prove the generalized mass action law together with the basic relations between kinetic factors, which are sufficient for the positivity of the entropy production but hold even without microreversibility, when the detailed balance is not applicable. Even though QE and QSS produce useful approximations by themselves, only the combination of these assumptions can render the possibility beyond the “rarefied gas” limit or the “molecular chaos” hypotheses. We do not use any a priori form of the kinetic law for the chemical reactions and describe their equilibria by thermodynamic relations. The transformations of the intermediate compounds can be described by the Markov kinetics because of their low density (low density of elementary events). This combination of assumptions was introduced by Michaelis and Menten in 1913. In 1952, Stueckelberg used the same assumptions for the gas kinetics and produced the remarkable semi-detailed balance relations between collision rates in the Boltzmann equation that are weaker than the detailed balance conditions but are still sufficient for the Boltzmann H-theorem to be valid. Our results are obtained within the Michaelis-Menten-Stueckelbeg conceptual framework.

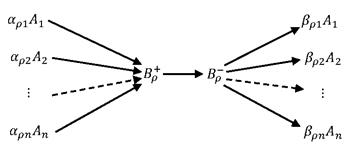
Горбань А.Н., Шахзад М., Теорема Михаелиса-Ментен-Штюкельберга. Entropy 2011, 13, 966-1019.

Рассматриваются сложные химические реакции при следующих предположениях: (1) промежуточные комплексы присутствуют в малых количествах (это соответствует гипотезе квазистационарности) и (2) они находятся в равновексных соотношениях с субстратами (это гипотеза квазиравновесия). При таких предположениях доказана применимость обобщенного закона действия масс для брутто реакций и существование соотношений между константами скорости, которые достаточны для положительности производства энтропии и верны даже в отсутствии микрообратимости, когда принцип детального равновесия не выполняется. Квазистационарность и квазиравновесие являются полезными приближениями по-отдельности, но только их комбинация дает такую возможность без обращения к приближению «разреженного газа» или «молекулярного хаоса». Такая комбинация предположений была предложена Михаелисом и Ментен в 1913 г. В 1952 г. Штюкельберг использовал тот же комплекс предположений для кинетики разреженного газа и доказал соотношения «полудетального равновесия» для ядер интеграла стокновения в уравнении Больцмана. Мы получаем наши результаты в продолжении работ Михаелиса-Ментен И Штюкельберга.

A.N. Gorban, G.S.Yablonsky Extended detailed balance for systems with irreversible reactions, Chemical Engineering Science 66 (2011) 5388–5399.

The principle of detailed balance states that in equilibrium each elementary process is equilibrated by its reverse process. For many real physico-chemical complex systems (e.g. homogeneous combustion, heterogeneous catalytic oxidation, most enzyme reactions etc), detailed mechanisms include both reversible and irreversible reactions. In this case, the principle of detailed balance cannot be applied directly. We represent irreversible reactions as limits of reversible steps and obtain the principle of detailed balance for complex mechanisms with some irreversible elementary processes. We proved two consequences of the detailed balance for these mechanisms: the structural condition and the algebraic condition that form together the extended form of detailed balance. The algebraic condition is the principle of detailed balance for the reversible part. The structural condition is: the convex hull of the stoichiometric vectors of the irreversible reactions has empty intersection with the linear span of the stoichiometric vectors of the reversible reaction. Physically, this means that the irreversible reactions cannot be included in oriented pathways.

The systems with the extended form of detailed balance are also the limits of the reversible systems with detailed balance when some of the equilibrium concentrations (or activities) tend to zero. Surprisingly, the structure of the limit reaction mechanism crucially depends on the relative speeds of this tendency to zero.

А.Н.Горбань, Г.С. Яблонский Расширенный принцип детального равновесия для систем, включающих необратимые реакции,Chemical Engineering Science 66 (2011) 5388–5399.

Принцип детального равновесия утверждает, что в равновесии каждый элементарный процесс уравновешивается своим обратным. Многие реальные физико-химические процессы (горение, гетерогенное каталитическое окисление, большинство ферментативных реакций и т.д.) включают одновременно м обратимые, и необратимые реакции. Для них принцип детального равновесия непосредственно не применим. Мы представляем необратимые реакции как пределыобратимых и полычаем в пределе принцип детального равновесия для систем, в которых часть реакций необратима. Мы доказали два следствия детального равновесия для таких механизмов реакции: структурные условия и алгебраические условия. Совместно они образуют расширенный принцип детального равновесия для систем, включающих необратимые реакции. Алгебраическое условие состоит в обычном принципе детального равновесия для обратимой части данного механизма реакции. Структурное условие формулируется так: выпуклая оболочка стехиометрических векторов необратимых реакций не пересекается с линейной оболочкой стехиометрических векторов обратимых реакций. Физически это означает, что необратимые реакции не могут принадлежать ориентированному циклическому маршруту реакции.

Системы с расширенным принципом детального равновесия являются также пределами обратимых систем с детальным равновесием, когда некоторые равновесные концентрации стремятся к нулю. Несколько неожиданно оказывается, что структура предельного механизма реакции зависит от относительных скоростей этого стремления к нулю.

NEW! A.N. Gorban, E.M. Mirkes, G.S. Yablonsky

Thermodynamics in the limit of irreversible reactions, [Термодинамика в пределе необратимых реакций] Physica A 392 (2013) 1318–1335.

For many complex real physicochemical systems, the detailed mechanism includes both reversible and irreversible reactions. Such systems are typical in homogeneous combustion and heterogeneous catalytic oxidation. Most complex enzyme reactions include irreversible steps. Classical thermodynamics has no limit for irreversible reactions, whereas kinetic equations may have such a limit. We represent systems with irreversible reactions as the limits of fully reversible systems when some of the equilibrium concentrations tend to zero. The structure of the limit reaction system crucially depends on the relative rates of this tendency to zero. We study the dynamics of the limit system and describe its limit behavior as t → ∞. If the reversible systems obey the principle of detailed balance then the limit system with some irreversible reactions must satisfy the extended principle of detailed balance. It is formulated and proven in the form of two conditions:
(i) the reversible part satisfies the principle of detailed balance and
(ii) the convex hull of the stoichiometric vectors of the irreversible reactions does not intersect the linear span of the stoichiometric vectors of the reversible reactions.
These conditions imply the existence of the global Lyapunov functionals and allow an algebraic description of the limit behavior. Thermodynamic theory of the irreversible limit of reversible reactions is illustrated by the analysis of hydrogen combustion.

NEW! A. N. Gorban, Thermodynamic Tree: The Space of Admissible Paths, [Термодинамическоедерево: пространство допустимых путей] SIAM J. Applied Dynamical Systems, Vol. 12, No. 1 (2013), pp. 246-278. DOI: 10.1137/120866919 arXiv e-print

Is a spontaneous transition from a state x to a state y allowed by thermodynamics? Such a question arises often in chemical thermodynamics and kinetics. We ask the more formal question: is there a continuous path between these states, along which the conservation laws hold, the concentrations remain non-negative and the relevant thermodynamic potential G (Gibbs energy, for example) monotonically decreases? The obvious necessary condition, G(x)≥G(y), is not sufficient, and we construct the necessary and sufficient conditions. For example, it is impossible to overstep the equilibrium in 1-dimensional (1D) systems (with n components and n-1 conservation laws). The system cannot come from a state x to a state y if they are on the opposite sides of the equilibrium even if G(x) > G(y). We find the general multidimensional analogue of this 1D rule and constructively solve the problem of the thermodynamically admissible transitions.

We study dynamical systems, which are given in a positively invariant convex polyhedron D and have a convex Lyapunov function G. An admissible path is a continuous curve along which $G$ does not increase. For x,y from D, x≥y (x precedes y) if there exists an admissible path from x to y and x~y if x≥y and y≥x. The tree of G in D is a quotient space D/~. We provide an algorithm for the construction of this tree. In this algorithm, the restriction of G onto the 1-skeleton of D (the union of edges) is used. The problem of existence of admissible paths between states is solved constructively. The regions attainable by the admissible paths are described.

NEW! B.M. Kaganovich, A.V. Keiko and V.A. Shamansky, Equilibrium Thermodynamic Modeling of Dissipative Macroscopic Systems [Равновесное термодинамическое моделирование диссипативных макроскопических систем], Advances in Chemical Engineering, Vol. 39, Thermodynamics and Kinetics of Complex Systems, 2010, pp. 1-75.

The possibility is substantiated to model open and closed systems as well as reversible and irreversible processes on the basis of classic equilibrium thermodynamics statements. The consideration is given to new modifications of the model of extreme intermediate states (MEIS) built originally in the mid-1980s. They include constraints on irreversible macroscopic kinetics presented in a thermodynamic form, i.e., without the time variable. MEIS is compared with models of chemical kinetics and irreversible thermodynamics from two viewpoints: (1) the range and versatility of application areas, and (2) the simplicity and self-descriptiveness of computational experiments. The potential of equilibrium modeling is explained on the examples of analysis of chemical systems and hydraulic circuits.

Родственные ресурсы:

Работы А.Н. Горбаня на Google scholar (цитирование > 5000)

Горбань и Карлин

Инвариантные многообразия в физической и химической кинетике

A.N. Gorban, I.V. Karlin, Invariant Manifolds for Physical and Chemical Kinetics,
Lect. Notes Phys. 660, Springer, Berlin, Heidelberg, 2005.

Этот сайт представляет читателям монографию «Инвариантные многообразия в физической и химической кинетике» и собрание совместных трудов А.Н. Горбаня и И.В. Карлина, вышедших в 1991-2007 гг.

Демон Дарвина

Сайт посвящен математическому моделированию биологической эволюции. Представлена книга

А.Н. Горбань, Р.Г. Хлебопрос, Демон Дарвина. Идея оптимальности и естественный отбор,

а также коллекция современных работ по проблемам эволюции, наследования, изменчивости.

Нелинейный Метод Главных Компонент

Представлена новая книга и большая коллекция статей по заглавной теме сайта.

Книга: A. Gorban, B. Kegl, D. Wunsch, A. Zinovyev  (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007. (ISBN 978-3-540-73749-0).
Главные многообразия для визуализации и анализа данных
Об этой книге
В 1901 г. Карл (Чарльз) Пирсон изобрел метод главных компонент. С тех пор, этот метод неоднократно служил прототипом для других изобретений в области анализа данных, их визуализации и сокращения описания. Таким образом, были созданы: метод независимых компонент, многомерное шкалирование, нелинейный метод главных компонент, самоорганизующиеся карты и многомерная топография данных.

Книга начинается с классического Пирсоновского определения главных компонент и включает обзор всех упомянутых методов, а также алгоритмов кластеризации. Также описаны новые подходы к нелинейному методу главных компонент, главным многообразиям, ветвящимся и локальным главным компонентам и отображениям, сохраняющим топологию данных. Описание методов и алгоритмов сопровождается детальным исследованием примеров из разных областей: от инженерных задач до астрономии. Большая часть примеров имеет биологическое происхождение: анализ генетических чипов и метаболических сетей. Том завершается учебной лекцией: "Метод главных компонент расшифровывает геном".

Last modified: May 24, 2011

Gorban
Alexander

in Encyclopaedia

"Russian Scientists"