Можно ли
обойти равновесие?
А.Н. Горбань ag153@le.ac.uk, Г.С.
Яблонский gy@seas.wustl.edu
Что не
запрещено, то разрешено. Так что же запрещено в ходе химических реакций,
теплопереноса и других диссипативных процессов? Можно ли «перебросить» систему
через равновесие, и если да, то на какую величину? На примере эффектов обхода
равновесия обсуждаются термодинамически разрешенные и запрещенные пути
процессов.
Is It Possible to Circumvent Equilibrium?
A.N. Gorban
ag153@le.ac.uk, G.S.Yablonskii gy@seas.wustl.edu
Everything
that is not prohibited is permissible. So, what is prohibited in the course of chemical reactions, heat
transfer and other dissipative processes? Is it possible to “overshoot” the
equilibrium, and if yes, then how far? Thermodynamically allowed and prohibited
trajectories of processes are discussed by the example of effects of
equilibrium encircling.
ОГЛАВЛЕНИЕ
Термодинамические
ограничения.
Ограничения,
связанные с механизмом реакции.
Введение
В начале было A, вещество A,
100% A в закрытом сосуде. Потом из A начало образовываться B. Появившись, B превращается обратно в A. Условия постоянны, скорости превращений пропорциональны
концентрациям. Система стремится к равновесию. Пусть для определенности в
равновесии концентрации A и B равны. Вопрос: может ли где-то по дороге к равновесию количество B в системе стать больше 50%? Ответ очевиден - нет. Если
концентрации A и B дойдут до 50% процентов, то
изменения прекратятся - это равновесие. Система одномерна - одна координата
(например, концентрация A)
полностью описывает состояние при фиксированных условиях - заданной температуре
и известном объеме. На прямой
обойти равновесие невозможно.
А если в системе есть еще вещество C? Что тогда - можно ли
обойти равновесие? Это первый вопрос. Ответ на него - «да». Поэтому возникает
второй: насколько сильно можно обойти равновесие в данном случае? Пусть (опять
же для определенности) равновесные концентрации A, B, и С равны друг
другу и все эти вещества могут превращаться друг в друга (являются изомерами).
Если нет специальных ограничений на механизм превращений, то для этой системы
обход равновесия возможен и если в начальный момент в системе 100% A, то по дороге к равновесию концентрация B не превышает верхней границы
![]() .
.
1. Теплообмен
Яркие примеры обхода равновесия можно получить,
рассматривая следующую задачу.
Задача. Два тела одинаковой
теплоемкости имеют различную температуру: ![]() (первое - горячее,
второе - холодное). Можно ли так организовать тепловой контакт между ними,
чтобы в результате теплопередачи горячее тело стало холодным, а холодное -
горячим? Возможен ли полный обмен
температурами (или почти полный)?
(первое - горячее,
второе - холодное). Можно ли так организовать тепловой контакт между ними,
чтобы в результате теплопередачи горячее тело стало холодным, а холодное -
горячим? Возможен ли полный обмен
температурами (или почти полный)?
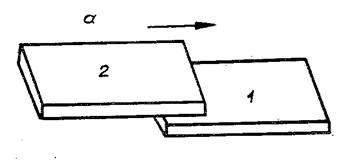
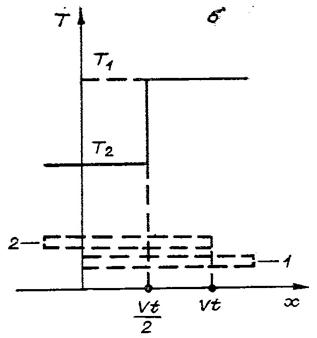
Рис.1. Скользящий контакт (а) и
распределение для него температуры по пластинам (б)
Решение. Пусть тела представляют
собой одинаковые тонкие прямоугольные пластины.
Проведем одну пластину по другой так, как показано на рис. 1.1, а. Пусть ![]() - длина пластины,
- длина пластины, ![]() - толщина,
- толщина, ![]() - температуропроводность
материала пластин. Если
- температуропроводность
материала пластин. Если ![]() достаточно велико, то
можно выбрать такую скорость
достаточно велико, то
можно выбрать такую скорость ![]() , что
, что
![]()
![]() (1)
(1)
(значок >> означает
«много больше»). Для такой скорости ![]() теплопереносом вдоль пластин
можно пренебречь, а теплопередачу по толщине пластин считать мгновенной. В
соответствии с этим положим температуру по толщине пластин считать постоянной,
температуру обеих пластин в точках контакта равной и запишем закон сохранения
энергии:
теплопереносом вдоль пластин
можно пренебречь, а теплопередачу по толщине пластин считать мгновенной. В
соответствии с этим положим температуру по толщине пластин считать постоянной,
температуру обеих пластин в точках контакта равной и запишем закон сохранения
энергии:
![]() (2)
(2)
![]()
Поскольку ![]()
![]() , из (2) получаем
, из (2) получаем
![]() (3)
(3)
при 0£vt£L (см. рис. 1, б). Аналогично (3) верно и при
![]() . Поэтому после прекращения контакта пластины поменяются
температурами. Обмен идет скачком ‑ в точке
. Поэтому после прекращения контакта пластины поменяются
температурами. Обмен идет скачком ‑ в точке ![]() происходит резкое
изменение температур. Фронт обмена движется со скоростью
происходит резкое
изменение температур. Фронт обмена движется со скоростью ![]() . Несомненно, в реальной ситуации этот фронт имеет конечную
ширину и разность температур после теплообмена меньше, чем до него, однако это
отличие («степень неупругости») может быть сколь угодно мало - по крайней мере в принципе.
. Несомненно, в реальной ситуации этот фронт имеет конечную
ширину и разность температур после теплообмена меньше, чем до него, однако это
отличие («степень неупругости») может быть сколь угодно мало - по крайней мере в принципе.
Устройства, реализующие принцип решения (противоток),
известны давно. Это обычные heat exchangers теплообменники. Тем не менее задачи подобного типа вызывают при первом знакомстве с
ними известные трудности. Даже квалифицированным физикам часто на первый взгляд
кажется, что «упругий» теплообмен принципиально невозможен. Это вызвано
«одномерной» интуицией - если фазовое пространство одномерно, то обойти
равновесие невозможно. Если бы температура обоих тел не изменялась от точки к
точке, то в отсутствие третьих тел состояние системы при фиксированных
начальных значениях ![]() однозначно описывалось
бы задаванием температуры одного из тел в силу сохранения энергии. В простейших
случаях при постоянной одинаковой теплоемкости
однозначно описывалось
бы задаванием температуры одного из тел в силу сохранения энергии. В простейших
случаях при постоянной одинаковой теплоемкости ![]() const.
const.
Рассмотрим подробнее двумерные системы (состояние -
точка на плоскости). Пусть температура одного тела пространственно однородна,
второе же состоит из двух половин, в каждой из которых температура также
пространственно однородна, а коэффициент теплопередачи между половинами мы
можем произвольно изменять от некоторой конечной величины до нуля.
Предположение о пространственной однородности означает, что перенос тепла
внутри тел (или, соответственно, половинок) происходит намного быстрее, чем
теплообмен между ними.
По сути здесь мы имеем дело с
тремя телами. Одно из них имеет теплоемкость с, два других (половины второго тела) - с/2. Обозначим их температуры
![]() . Предполагается, что как в начальном, так и в конечном
состоянии
. Предполагается, что как в начальном, так и в конечном
состоянии ![]() . Закон сохранения энергии дает
. Закон сохранения энергии дает ![]() const. Поэтому для описания системы при заданной энергии
достаточно двух температур. Воспользовавшись законом сохранения, можно выразить
const. Поэтому для описания системы при заданной энергии
достаточно двух температур. Воспользовавшись законом сохранения, можно выразить
![]() через
через
![]() :
: ![]() , где
, где ![]()
![]() - температура в начальном состоянии. Плоскость с декартовыми
координатами
- температура в начальном состоянии. Плоскость с декартовыми
координатами ![]() разобьем линиями частных равновесий - тремя прямыми с
уравнениями
разобьем линиями частных равновесий - тремя прямыми с
уравнениями ![]() и
и ![]() . Эти прямые пересекаются в одной точке равновесия, где
. Эти прямые пересекаются в одной точке равновесия, где ![]() , и разделяют плоскость на 6 углов
, и разделяют плоскость на 6 углов ![]() (рис. 2). Далее такие
углы называются отсеками. Каждый
отсек соответствует одной расстановке знаков в неравенствах между
(рис. 2). Далее такие
углы называются отсеками. Каждый
отсек соответствует одной расстановке знаков в неравенствах между
![]() и
и ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]() из следующих:
из следующих:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
Возможны еще два способа расстановки знаков в этих
неравенствах: ![]() и
и ![]() , но они внутренне противоречивы, и им не соответствует ни
один отсек.
, но они внутренне противоречивы, и им не соответствует ни
один отсек.
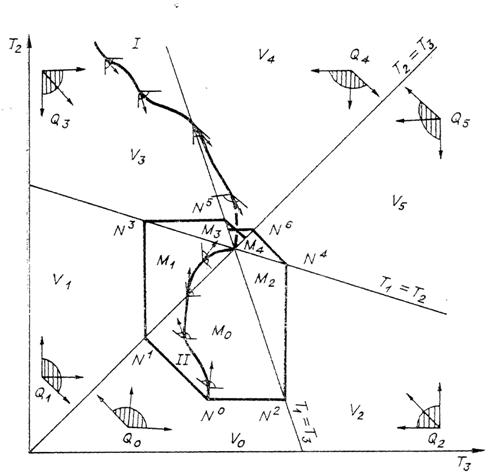
Рис. 2. Отсеки ![]() , углы возможных направлений
, углы возможных направлений ![]() (заштрихованы),
примеры допустимых путей (I,
II) и
множество состояний, достижимых из данного начального
(заштрихованы),
примеры допустимых путей (I,
II) и
множество состояний, достижимых из данного начального ![]() (область с выделенной
границей), для теплообмена трех тел, если одно из них имеет теплоемкость с, два других - с/2.
(область с выделенной
границей), для теплообмена трех тел, если одно из них имеет теплоемкость с, два других - с/2.
Рассмотрим движение системы при наличии контактов
между телами. Если приведены в контакт первое и второе тело,
а третье изолировано, то движение происходит вдоль прямой ![]() const по направлению к точке ее пересечения с прямой
const по направлению к точке ее пересечения с прямой ![]() . Аналогично и для других контактов. В каждом отсеке
есть тройка направлений движения, соответствующая трем парным контактам (рис.
2).
. Аналогично и для других контактов. В каждом отсеке
есть тройка направлений движения, соответствующая трем парным контактам (рис.
2).
Возможное направление движения
системы
есть сумма с положительными коэффициентами направляющих векторов для парных
контактов. В каждом отсеке однозначно определен угол возможных направлений ![]() . Кривая с выделенным направлением движения есть допустимый
путь перемещения системы, если в каждой ее точке касательный вектор,
ориентированный по направлению движения, лежит в угле возможных направлений
(рис. 2). Угол возможных направлений выбирается в соответствии с тем отсеком,
где лежит точка. Линия частичного равновесия считается принадлежащей обоим
пограничным с ней отсекам, а угол возможных направлений для лежащих на ней
точек есть пересечение углов, соответствующих прилегающим отсекам.
. Кривая с выделенным направлением движения есть допустимый
путь перемещения системы, если в каждой ее точке касательный вектор,
ориентированный по направлению движения, лежит в угле возможных направлений
(рис. 2). Угол возможных направлений выбирается в соответствии с тем отсеком,
где лежит точка. Линия частичного равновесия считается принадлежащей обоим
пограничным с ней отсекам, а угол возможных направлений для лежащих на ней
точек есть пересечение углов, соответствующих прилегающим отсекам.
Для каждого начального состояния построим область
состояний, в которые можно попасть из него, двигаясь по допустимым путям (область достижимости). Пусть ![]() - начальное состояние
(рис. 2),
- начальное состояние
(рис. 2), ![]() лежит в отсеке
лежит в отсеке ![]() - соответствующий угол
возможных направлений. Перенесем вершину этого угла в точку
- соответствующий угол
возможных направлений. Перенесем вершину этого угла в точку ![]() и рассмотрим его
пересечение с
и рассмотрим его
пересечение с ![]() . Обозначим
. Обозначим ![]() и
и ![]() наиболее удаленные от
равновесия точки этого множества, лежащие на граничных прямых
наиболее удаленные от
равновесия точки этого множества, лежащие на граничных прямых ![]() . Соответствующие соседние отсеки обозначим
. Соответствующие соседние отсеки обозначим ![]() , а углы возможных направлений -
, а углы возможных направлений - ![]() . Перенесем вершины углов
. Перенесем вершины углов ![]() в точки
в точки ![]() и рассмотрим их
пересечения с
и рассмотрим их
пересечения с ![]() соответственно
соответственно ![]() и
и ![]() . В этих множествах есть точки, лежащие на прямых,
ограничивающих
. В этих множествах есть точки, лежащие на прямых,
ограничивающих ![]() и не примыкающих
к
и не примыкающих
к ![]() . Выберем из них самые далекие от равновесия
и повторим построение (рис. 2). Будем повторять описанное построение до
тех пор, пока после очередного шага не перестанут появляться новые точки.
Получим множество
. Выберем из них самые далекие от равновесия
и повторим построение (рис. 2). Будем повторять описанное построение до
тех пор, пока после очередного шага не перестанут появляться новые точки.
Получим множество ![]() . Это множество всех состояний, достижимых из
. Это множество всех состояний, достижимых из
![]() .
.
По условию исходной задачи в начальный и конечный
моменты ![]() . Обозначая температуры в конечном состоянии
. Обозначая температуры в конечном состоянии ![]() и повторяя построения
рис. 2, получим (рис. 3): если
и повторяя построения
рис. 2, получим (рис. 3): если ![]() , то
, то
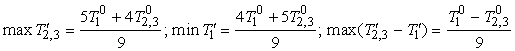 . (4)
. (4)
Способ реализации (4) таков: первое тело приводится в
равновесие с одной половиной второго, их температура становится равной ![]() . Затем первое тело приводится в равновесие со второй
половиной и приобретает температуру
. Затем первое тело приводится в равновесие со второй
половиной и приобретает температуру ![]() . Затем в равновесие приходят половины между собой. Их
конечная температура
. Затем в равновесие приходят половины между собой. Их
конечная температура ![]() .
.
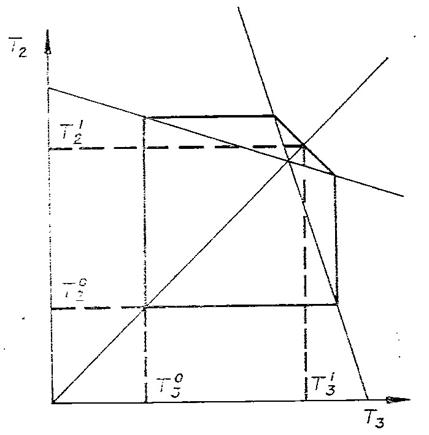
Рис. 2. Теплообмен трех тел с
максимальным эффектом обхода равновесия; в начальный и конечный моменты ![]() .
.
2. Закон действия масс
При описании кинетики химической реакции представляют
сложную реакцию как совокупность простых (элементарных), а скорости простых
реакций находят по сравнительно простому правилу. В простейшем случае скорость элементарной
реакции задается законом действия масс. Такие простейшие системы называются кинетически идеальными. Элементарная
реакция задается своим стехиометрическим
уравнением
![]() , (5)
, (5)
здесь ![]() - символы веществ,
- символы веществ, ![]() - стехиометрические коэффициенты - целые числа, показывающие, сколько
молекул
- стехиометрические коэффициенты - целые числа, показывающие, сколько
молекул ![]() участвует в одном акте
элементарной реакции в качестве исходного реагента
участвует в одном акте
элементарной реакции в качестве исходного реагента ![]() и в качестве продукта
и в качестве продукта ![]() . В (5) одновременно записаны как прямая, так и обратная
реакции (направление реакции указывается стрелкой). Для обратной реакции
. В (5) одновременно записаны как прямая, так и обратная
реакции (направление реакции указывается стрелкой). Для обратной реакции ![]() - число молекул
- число молекул ![]() , участвующих в одном акте реакции в качестве исходного
реагента,
, участвующих в одном акте реакции в качестве исходного
реагента, ![]() - число молекул
- число молекул ![]() , получающихся в одном акте реакции в качестве продукта. По
закону действия масс скорости прямой
, получающихся в одном акте реакции в качестве продукта. По
закону действия масс скорости прямой ![]() и обратной
и обратной ![]() реакции суть
реакции суть
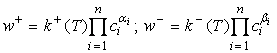 (6)
(6)
где ![]() - концентрация
- концентрация ![]() - температура,
- температура, ![]() - константы скорости.
Число различных констант скорости равно
- константы скорости.
Число различных констант скорости равно ![]() , где
, где ![]() - количество различных
элементарных стадий (взаимно обратных
элементарных реакций (5)). Однако не всегда эти
- количество различных
элементарных стадий (взаимно обратных
элементарных реакций (5)). Однако не всегда эти ![]() констант можно
задавать независимо.
констант можно
задавать независимо.
Ограничения на возможные значения констант могут быть
сформулированы в виде принципа детального
равновесия: для каждого T существует такой набор положительных концентраций ![]() (точка равновесия),
что
(точка равновесия),
что
![]() . (7)
. (7)
Существование такой точки детального равновесия влечет многочисленные следствия. В частности,
оно связано с постоянным убыванием в ходе реакции некоторых функций. Так, для
реакций, осуществляемых при постоянных объеме и
температуре, монотонно уменьшается функция
![]() . (8)
. (8)
Действительно, для реакции при указанных условиях
дифференциальные уравнения, которым подчиняется динамика концентраций ![]() , имеют вид (точкой над буквой обозначается производная по
времени):
, имеют вид (точкой над буквой обозначается производная по
времени):
![]() . (9)
. (9)
где ![]() - номер стадии,
величины с индексом
- номер стадии,
величины с индексом ![]() соответствуют
соответствуют ![]() -й стадии,
-й стадии, ![]() .
.
В силу этих уравнений (9) функция (8) меняется по
следующему закону:
![]() . (10)
. (10)
Последнее неравенство
очевидно: для любых положительных a, b ![]() из-за того, что ln - возрастающая функция.
из-за того, что ln - возрастающая функция.
Будем рассматривать только закрытые идеальные
химические системы и реакции при постоянных объеме и
температуре. Для них роль второго начала термодинамики играет утверждение:
функция ![]() (8) в ходе химической
реакции должна убывать (не возрастать).
(8) в ходе химической
реакции должна убывать (не возрастать).
3. Изомеризация
Если реагирующая смесь состоит только из двух веществ
- изомеров ![]() , то система все время движется к равновесию, а перейти его
не в состоянии: пусть равновесные концентрации
, то система все время движется к равновесию, а перейти его
не в состоянии: пусть равновесные концентрации ![]() суть
суть ![]() , тогда
, тогда ![]() монотонно приближаются
к
монотонно приближаются
к ![]() . При наличии большого числа веществ такого простого
ограничения на динамику уже нет. Тем не менее возможный
вид функции
. При наличии большого числа веществ такого простого
ограничения на динамику уже нет. Тем не менее возможный
вид функции ![]() (
(![]() - концентрация i-го вещества) не произволен
и аналог монотонности существует. Это связано с существованием убывающих со
временем функций состава.
- концентрация i-го вещества) не произволен
и аналог монотонности существует. Это связано с существованием убывающих со
временем функций состава.
Термодинамические
ограничения. Предполагается, что система
состоит из n изомеров ![]() и идеальна. При
указанных условиях со временем должны убывать функция G (8). С точностью до
постоянных множителей и слагаемых G - свободная энергия системы.
и идеальна. При
указанных условиях со временем должны убывать функция G (8). С точностью до
постоянных множителей и слагаемых G - свободная энергия системы.
Если ![]() - моменты времени и
- моменты времени и ![]() , то
, то ![]() . Здесь
. Здесь ![]() - вектор (набор)
концентраций в момент t.
Но неравенство
- вектор (набор)
концентраций в момент t.
Но неравенство ![]() - не единственное
ограничение на возможное значение
- не единственное
ограничение на возможное значение ![]() при
данном
при
данном ![]() . В одномерном случае (два изомера, один закон сохранения
. В одномерном случае (два изомера, один закон сохранения ![]() ) точка должна лежать по ту же сторону равновесия, что и
) точка должна лежать по ту же сторону равновесия, что и ![]() : если
: если ![]() , то и
, то и ![]() , а если
, а если ![]() , то
, то ![]() .
.
Чтобы получить аналог этого ограничения для числа
веществ ![]() , обратимся к исследованию термодинамически допустимых путей реакции. В рассматриваемом случае
это такие непрерывные кривые
, обратимся к исследованию термодинамически допустимых путей реакции. В рассматриваемом случае
это такие непрерывные кривые ![]() , что:
, что:
а) ![]() для всех
для всех ![]() ,
,
б) выполняется балансное ограничение ![]() ,
,
в) ![]() - монотонно убывающая
функция t.
- монотонно убывающая
функция t.
Переход из точки ![]() в точку
в точку ![]() называется термодинамически разрешенным (при данных условиях), если
существует термодинамически допустимый путь реакции
называется термодинамически разрешенным (при данных условиях), если
существует термодинамически допустимый путь реакции ![]() , для которого
, для которого ![]() при
некотором
при
некотором ![]() . В противном случае такой переход считается термодинамически
запрещенным.
. В противном случае такой переход считается термодинамически
запрещенным.
Для изучения термодинамически
запрещенных переходов оказывается полезным рассмотреть поверхности уровня
функции G, задаваемые уравнениями ![]() . При некоторых g эти поверхности становятся несвязными -распадаются
на отдельные куски (связные компоненты), лежащие в симплексе
. При некоторых g эти поверхности становятся несвязными -распадаются
на отдельные куски (связные компоненты), лежащие в симплексе ![]() , и разрезающие его, каждая - на две части. В одной из этих частей
, и разрезающие его, каждая - на две части. В одной из этих частей ![]() , в другой есть точки, где
, в другой есть точки, где ![]() (в частности, точка
равновесия
(в частности, точка
равновесия ![]() ), но в ней могут быть и такие
), но в ней могут быть и такие ![]() , что
, что ![]() . Траектория системы, начинающаяся в такой
. Траектория системы, начинающаяся в такой ![]() , не может пересечь соответствующую связную компоненту
поверхности уровня - для этого на каком-то участке движения должна была бы
нарушиться монотонность изменения
, не может пересечь соответствующую связную компоненту
поверхности уровня - для этого на каком-то участке движения должна была бы
нарушиться монотонность изменения ![]() . Поэтому возможна следующая ситуация:
. Поэтому возможна следующая ситуация: ![]() , но не существует такой непрерывной кривой
, но не существует такой непрерывной кривой ![]() , что
, что ![]() - монотонно убывающая
функция. Проиллюстрируем это графически, предельно упростив систему: пусть
изомеров всего три (
- монотонно убывающая
функция. Проиллюстрируем это графически, предельно упростив систему: пусть
изомеров всего три (![]() ), а их равновесные концентрации равны (
), а их равновесные концентрации равны (![]() ). При фиксированном значении баланса
). При фиксированном значении баланса ![]() состояние системы
изображается точкой, лежащей в треугольнике
состояние системы
изображается точкой, лежащей в треугольнике ![]() . Этот треугольник представляет собой сечение положительного
октанта плоскостью. Его удобно изображать равносторонним треугольником на
плоскости (рис. 4, а) с высотой
. Этот треугольник представляет собой сечение положительного
октанта плоскостью. Его удобно изображать равносторонним треугольником на
плоскости (рис. 4, а) с высотой ![]() (стороной
(стороной ![]() ). Если состояние системы изображается вершиной треугольника,
это означает, что в системе присутствует только один изомер:
). Если состояние системы изображается вершиной треугольника,
это означает, что в системе присутствует только один изомер: ![]() , либо
, либо ![]() , либо
, либо ![]() . На рис. 4 для каждой вершины указано соответствующее
вещество. Концентрация
. На рис. 4 для каждой вершины указано соответствующее
вещество. Концентрация ![]() есть длина
перпендикуляра, опущенного из точки c
(изображающей состояние) на строну, противоположную
вершине
есть длина
перпендикуляра, опущенного из точки c
(изображающей состояние) на строну, противоположную
вершине ![]() (той вершине, где
(той вершине, где ![]() ). Рассмотрим линии уровня функции G (8). Если g близко к
). Рассмотрим линии уровня функции G (8). Если g близко к
![]() , то линия
, то линия ![]() связна (рис. 4, б).
Однако если g становится больше минимума
связна (рис. 4, б).
Однако если g становится больше минимума ![]() на ребрах
треугольника, но остается меньше максимума
на ребрах
треугольника, но остается меньше максимума ![]() в треугольнике, то
линия
в треугольнике, то
линия ![]() распадается на три
связные части (рис. 4, б).
распадается на три
связные части (рис. 4, б).
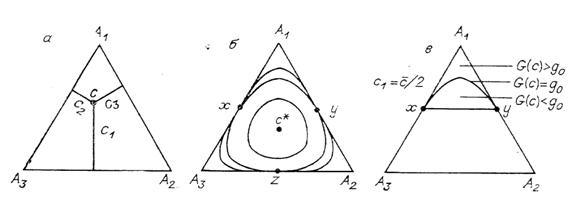
Рис. 4. Три изомера: а – система координат, б – линии уровня G, в – область
недоступности вблизи ![]() .
.
Минимум ![]() на ребрах треугольника
достигается на их серединах, совпадает для всех ребер (так как
на ребрах треугольника
достигается на их серединах, совпадает для всех ребер (так как ![]() ) и равен
) и равен ![]() . Дуги линии уровня
. Дуги линии уровня ![]() , соединяющие середины ребер, образуют непроходимые границы -
невозможность пересечь их «изнутри» есть аналог невозможности перехода
равновесия, но уже для двумерной системы. Весь треугольник разбивается на
четыре области (рис. 4, б): треугольники
, соединяющие середины ребер, образуют непроходимые границы -
невозможность пересечь их «изнутри» есть аналог невозможности перехода
равновесия, но уже для двумерной системы. Весь треугольник разбивается на
четыре области (рис. 4, б): треугольники ![]() (одна сторона каждого
из них есть участок кривой
(одна сторона каждого
из них есть участок кривой ![]() ) и область
) и область ![]() . Ни одна точка (
. Ни одна точка (![]() ) из внутренности какого-либо из этих криволинейных треугольников
не может быть связана ни с какой внутренней точкой (
) из внутренности какого-либо из этих криволинейных треугольников
не может быть связана ни с какой внутренней точкой (![]() ) другого криволинейного треугольника термодинамически
допустимым путем (вдоль которого G не
возрастает). Это невозможно даже в том случае, когда
) другого криволинейного треугольника термодинамически
допустимым путем (вдоль которого G не
возрастает). Это невозможно даже в том случае, когда ![]() , - все равно по дороге от
, - все равно по дороге от ![]() к
к ![]() траектория должна
пересечь «изнутри» (со стороны меньших значений G) одну из
дуг кривой
траектория должна
пересечь «изнутри» (со стороны меньших значений G) одну из
дуг кривой ![]() (рис. 4, б).
Допустимость перемещений внутри треугольников и в области
(рис. 4, б).
Допустимость перемещений внутри треугольников и в области ![]() определяется по
справедливости неравенства
определяется по
справедливости неравенства ![]() . Пусть выполнено одно из следующих условий:
. Пусть выполнено одно из следующих условий:
а) ![]() и
и ![]() лежат обе в одном из
криволинейных треугольников
лежат обе в одном из
криволинейных треугольников ![]() ;
;
б) ![]() лежит в одном из
криволинейных треугольников
лежит в одном из
криволинейных треугольников ![]() , а
, а ![]() - в области
- в области ![]() ;
;
в) ![]() -
-
тогда перемещение из ![]() в
в ![]() термодинамически
разрешено в том и только в том случае, когда
термодинамически
разрешено в том и только в том случае, когда ![]() . Более того, поскольку перемещение из одного криволинейного
треугольника в другой запрещено, здесь перечислены все возможные случаи
разрешенных перемещений в треугольнике.
. Более того, поскольку перемещение из одного криволинейного
треугольника в другой запрещено, здесь перечислены все возможные случаи
разрешенных перемещений в треугольнике.
Вблизи каждой вершины есть область (примыкающий
криволинейный треугольник), в которую невозможно попасть извне. Возникает
интересный вопрос: насколько можно приблизиться к данной вершине (для
определенности ![]() ), если начальное состояние задано. Пусть начальные
концентрации суть
), если начальное состояние задано. Пусть начальные
концентрации суть ![]() , требуется найти
, требуется найти ![]() , где
, где ![]() - состояние, в которое
можно перейти из
- состояние, в которое
можно перейти из ![]() , и верхняя грань берется по всем таким состояниям
, и верхняя грань берется по всем таким состояниям ![]() . Геометрически ясно (рис. 4, б), что
. Геометрически ясно (рис. 4, б), что ![]() надо искать таким
образом:
надо искать таким
образом:
а) если ![]() лежит в
лежит в ![]() или в
области
или в
области ![]() , то
, то ![]() есть максимум
есть максимум ![]() на линии
на линии ![]() ;
;
б) если ![]() лежит в
лежит в ![]() или
или ![]() , то
, то ![]() есть максимум
есть максимум ![]() на линии
на линии ![]() .
.
Чтобы найти ![]() для данного
для данного ![]() , надо уметь находить указанные максимумы и, кроме того,
иметь аналитические критерии принадлежности точки
, надо уметь находить указанные максимумы и, кроме того,
иметь аналитические критерии принадлежности точки ![]() той или иной области. Эти
критерии выглядят так:
той или иной области. Эти
критерии выглядят так: ![]() лежит в области
лежит в области ![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]() лежит в
лежит в ![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]()
![]() лежит в
лежит в ![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]()
![]() лежит в
лежит в ![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]()
![]() . Критерий принадлежности
. Критерий принадлежности ![]() , например,
, например, ![]() получен так (рис. 4,
в): криволинейный треугольник
получен так (рис. 4,
в): криволинейный треугольник ![]() состоит из тех и
только тех точек прямоугольного треугольника
состоит из тех и
только тех точек прямоугольного треугольника ![]() , в которых
, в которых ![]() .
.
Из симметрии системы ясно, что ![]() на линии уровня
на линии уровня ![]() достигается на прямой
достигается на прямой ![]() . Точки пересечения этой прямой с линией уровня
. Точки пересечения этой прямой с линией уровня ![]() находятся из уравнения
находятся из уравнения
![]() (11)
(11)
На рис. 5, а представлена зависимость ![]() от
от
![]() для решения (11):
для решения (11): ![]() .
.
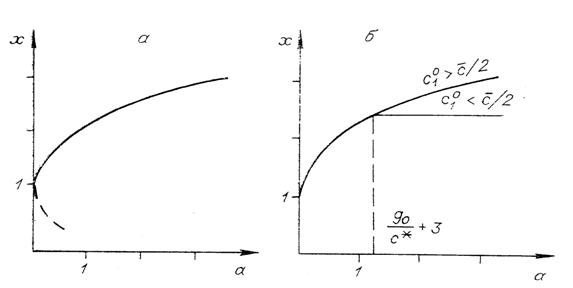
Рис. 5. Решения уравнения (11) (а) и две ветви
зависимости ![]() от
от ![]() (б).
(б).
Используя решение (11), можно найти, как изменяется ![]() в зависимости от
в зависимости от ![]() (рис. 5, б). При
(рис. 5, б). При ![]() эта зависимость
однозначна. Если
эта зависимость
однозначна. Если ![]() , то возможны два варианта: при
, то возможны два варианта: при ![]() (
(![]() лежит в
лежит в ![]() или
или ![]() )
) ![]() равен максимуму
равен максимуму ![]() на линии
на линии ![]() (нижняя ветвь графика
на рис. 5, б), если же
(нижняя ветвь графика
на рис. 5, б), если же ![]() , то зависимость
, то зависимость ![]() от
от ![]() дается решением
уравнения (11) (верхняя ветвь графика на рис. 5, б).
дается решением
уравнения (11) (верхняя ветвь графика на рис. 5, б).
В одномерной системе (два изомера) с единичной
константой равновесия (![]() ) невозможность перехода через равновесие можно в наших
обозначениях сформулировать так: если
) невозможность перехода через равновесие можно в наших
обозначениях сформулировать так: если ![]() , то
, то ![]() . В только что разобранном двумерном случае возможно
аналогичное утверждение, но с другими коэффициентами: если
. В только что разобранном двумерном случае возможно
аналогичное утверждение, но с другими коэффициентами: если ![]() то
то ![]() (
(![]() приближенное значение решения (11) при
приближенное значение решения (11) при
![]() ).
).
Ограничения, связанные
с механизмом реакции. Термодинамические
ограничения определяются только списком реагентов, положением точки равновесия
и видом функции G (8). Они будут справедливы даже
в том случае, если допускаются элементарные стадии, скажем, вида ![]() . Как правило, таких элементарных реакций не бывает. Сокращая
список возможных элементарных стадий до разумного, мы,
естественно, сужаем множество возможных путей реакции по сравнению с
термодинамически допустимыми путями. Исследуем возникающие в системе трех
изомеров ограничения, связанные с тремя механизмами реакции:
. Как правило, таких элементарных реакций не бывает. Сокращая
список возможных элементарных стадий до разумного, мы,
естественно, сужаем множество возможных путей реакции по сравнению с
термодинамически допустимыми путями. Исследуем возникающие в системе трех
изомеров ограничения, связанные с тремя механизмами реакции:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Пусть, как и выше, ![]() . Для каждой стадии существует поверхность (в этом примере -
линия) равновесия, на которой прямая реакция уравновешивается обратной. Для
стадии
. Для каждой стадии существует поверхность (в этом примере -
линия) равновесия, на которой прямая реакция уравновешивается обратной. Для
стадии ![]() она в данном примере
задается уравнением
она в данном примере
задается уравнением ![]() . Линии равновесия стадий разбивают треугольник
. Линии равновесия стадий разбивают треугольник ![]() на отсеки, в которых однозначно определено
направление каждой реакции - прямое или обратное (рис. 6, а-в). Стадия
на отсеки, в которых однозначно определено
направление каждой реакции - прямое или обратное (рис. 6, а-в). Стадия ![]() сдвигает систему вдоль
прямой
сдвигает систему вдоль
прямой ![]() по направлению к линии
равновесия
по направлению к линии
равновесия ![]() . Аналогично к своим линиям равновесия сдвигают систему и
другие стадии. Если механизм реакции одностадийный, то движение происходит по прямой. Внутри данного отсека каждой стадии
сопоставляется вектор, направленный вдоль этой прямой к линии равновесия. Для многостадийных сложных реакций возможное направление
движения есть комбинация с положительными коэффициентами направляющих векторов
всех стадий. Внутри каждого отсека множество таких комбинаций образует угол - угол возможных направлений движения (см.
Рис. 6, а-г для различных
механизмов реакции). Если же точка лежит на линии равновесия какой-нибудь
стадии, то ей сопоставляется угол, совпадающий с пересечением углов прилегающих
отсеков.
. Аналогично к своим линиям равновесия сдвигают систему и
другие стадии. Если механизм реакции одностадийный, то движение происходит по прямой. Внутри данного отсека каждой стадии
сопоставляется вектор, направленный вдоль этой прямой к линии равновесия. Для многостадийных сложных реакций возможное направление
движения есть комбинация с положительными коэффициентами направляющих векторов
всех стадий. Внутри каждого отсека множество таких комбинаций образует угол - угол возможных направлений движения (см.
Рис. 6, а-г для различных
механизмов реакции). Если же точка лежит на линии равновесия какой-нибудь
стадии, то ей сопоставляется угол, совпадающий с пересечением углов прилегающих
отсеков.
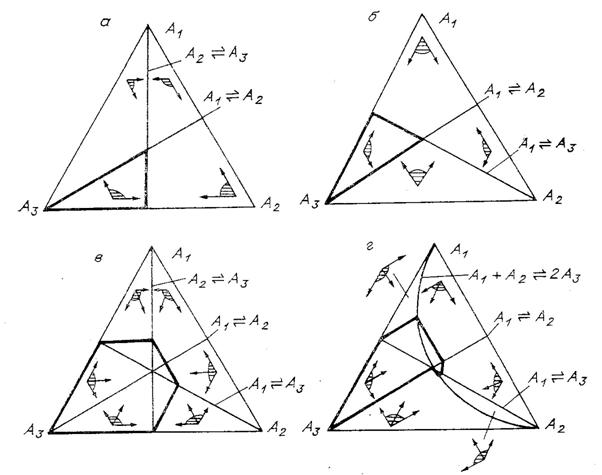
Рис. 6. Рис. 6. Составы,
достижимые из ![]() (области с выделенной
границей), для различных механизмов реакции:
(области с выделенной
границей), для различных механизмов реакции:
а - ![]() ,
,
б - ![]() ,
,
в - ![]() ,
,
г - ![]() ;
;
указаны линии равновесия стадий и углы возможных направлений (заштрихованы).
Гладкая кривая ![]() есть допустимый путь
реакции, если
есть допустимый путь
реакции, если
а) ![]() для любых
для любых ![]() ;
;
б) ![]() ;
;
в) касательный вектор ![]() принадлежит углу
возможных направлений, соответствующему точке
принадлежит углу
возможных направлений, соответствующему точке ![]() (см. рис. 6).
(см. рис. 6).
Описанные допустимые пути и
термодинамически допустимы - вдоль них монотонно убывает функция ![]() . Переход в ходе реакции от состава
. Переход в ходе реакции от состава ![]() к составу
к составу ![]() допустим тогда и
только тогда, когда существует такой допустимый путь
допустим тогда и
только тогда, когда существует такой допустимый путь ![]() , что
, что ![]() для некоторого
для некоторого ![]() . Пусть задано
. Пусть задано ![]() . Так же, как и для теплообмена (см. первый раздел и рис. 2),
построим множество тех
. Так же, как и для теплообмена (см. первый раздел и рис. 2),
построим множество тех ![]() , для которых допустим переход от
, для которых допустим переход от ![]() к
к ![]() .
.
На рис. 6, а-в изображены множества достижимых
состояний M для различных механизмов
реакции и начального состояния ![]() . Для механизмов
. Для механизмов ![]() множество M при таком начальном
состоянии совпадает с
множество M при таком начальном
состоянии совпадает с ![]() (рис. 6, а, б). Для
большего механизма
(рис. 6, а, б). Для
большего механизма ![]() множество M существенно шире (рис. 6,
в). Для механизма
множество M существенно шире (рис. 6,
в). Для механизма ![]() и данного начального
состояния значение
и данного начального
состояния значение ![]() не превосходит
не превосходит ![]() . Для двух других рассматриваемых механизмов реакции
. Для двух других рассматриваемых механизмов реакции ![]() не превосходит
не превосходит ![]() (как и в одномерном
случае).
(как и в одномерном
случае).
Покажем все на том же примере (три изомера, ![]() ), каким образом наличие стадии с взаимодействием
различных веществ позволяет обойти равновесие (точнее, снимает запрет).
Дополним механизм реакции
), каким образом наличие стадии с взаимодействием
различных веществ позволяет обойти равновесие (точнее, снимает запрет).
Дополним механизм реакции ![]() стадией
стадией ![]() (механизм (г)). Ее
линия равновесия задается уравнением
(механизм (г)). Ее
линия равновесия задается уравнением ![]() (все при том же условии
(все при том же условии
![]() ). В силу реакции
). В силу реакции ![]() система движется вдоль
прямой, параллельной биссектрисе угла
система движется вдоль
прямой, параллельной биссектрисе угла ![]() (рис. 6, г).
Направляющий вектор имеет компоненты (1, 1, -2). Максимальное значение
(рис. 6, г).
Направляющий вектор имеет компоненты (1, 1, -2). Максимальное значение ![]() для
для
![]() дает допустимый путь, состоящий из двух прямолинейных отрезков -
движения от
дает допустимый путь, состоящий из двух прямолинейных отрезков -
движения от ![]() к точке
к точке ![]() вдоль линии
вдоль линии ![]() и движения от этой
точки вдоль прямой, параллельной биссектрисе угла
и движения от этой
точки вдоль прямой, параллельной биссектрисе угла ![]() , к линии равновесия стадии
, к линии равновесия стадии ![]() . Этот путь можно интерпретировать следующим образом: вначале
приходит в равновесие стадия
. Этот путь можно интерпретировать следующим образом: вначале
приходит в равновесие стадия ![]() , потом
, потом ![]() . Значение
. Значение ![]() в конце пути есть
в конце пути есть ![]() .
.
Таким образом, при наличии в механизме реакции стадии
с взаимодействием различных веществ обход равновесия не запрещен. Для каждого
конкретного механизма реакции множество допустимых путей (и достижимых
состояний) уже, чем множество термодинамически допустимых путей.
Заключение
Общие запреты для направлений протекания процессов,
общие ограничения на величину различных эффектов дают нам принципы
термодинамики.
И в жизни, и в науке принципы нужны для уничтожения
гипотез, идей, конструкций. Так, закон сохранения энергии связан с уничтожением
вечных двигателей первого рода (черпающих энергию из ничего), второе начало
термодинамики - с уничтожением вечных двигателей второго рода (черпающих
энергию из равновесно распределенного тепла). Принципы - средство массового
уничтожения: истребляются сразу все упомянутые конструкции. И невозможно, и не
нужно обсуждать новые вечные двигатели - для этого надо сначала всерьез
уничтожить принципы термодинамики.
Но столь серьезное средство нуждается в столь же
внимательном и бережном отношении. Рассмотрение эффектов обхода равновесия
позволит яснее понять, как устроены термодинамические ограничения на динамику
неравновесных систем, что запрещено, а что – нет.
Литература
1. Пригожин И., Дефей Р. Химическая термодинамика. Новосибирск: Наука,
1966. 510 с. (Прекрасное изложение базовых понятий термодинамики.)
2. Gorban A.N. Invariant sets for kinetic equations // React. Kinet. Catal. Lett., 1978. V. 10, №
2. PP. 187-190. (Первая работа по областям достижимости и
допустимым путям.)
3. Горбань А.Н.,
Яблонский Г.С., Быков В.И. Путь к равновесию // Математические проблемы
химической термодинамики. Новосибирск: Наука, 1980. С. 37-47. (Первая подробная статья.)
4.
Gorban A.N., Jablonsky
G.S., Bykov V.I. The path to equilibrium // Intern.
Chem.
5. Горбань А.Н. Обход равновесия. Новосибирск: Наука,
1984. 224 с. (Первое детальное изложение теории термодинамических ограничений и
эффектов обхода равновесия.)
6. Shinnar R., Feng C., Structure of complex chemical
reactions. Thermodynamic constrains in
kinetic modeling and catalyst evaluation, Ind. and Eng. Chem. Fund., V. 24
(1985), No. 2, 153-170. (Изложение теории термодинамических ограничений
на простейших примерах.)
7. Shinnar R., Thermodynamic analysis in chemical process and reactor design,
Chem. Eng. Sci., 43, Iss.
8 (1988), 2303-2318. (Изложены принципы приложения теории термодинамических ограничений к
конструированию реакторов на простейших примерах.)
8. Vuddagiri S.R., Hall K.R., Eubank Ph.T., Dynamic modeling of reaction pathways on the Gibbs energy surface.
9. Каганович
Б.М., Кучменко Е.В., Шаманский В.А., Ширкалин И.А. Термодинамическое моделирование фазовых
переходов в многокомпонентных системах // Изв.
РАН. Энергетика. – 2005. – № 2. – С. 114-121.
10.Каганович
Б.М., Кейко А.В., Шаманский В.А., Ширкалин
И.А. Описание неравновесных процессов в энергетических задачах методами
равновесной термодинамики // Изв. РАН. Энергетика.
– 2006. – № 3. – С. 64-75.
11.Gorban A.N., Kaganovich B.M., Fillipov S.P., Keiko
A.V., Shamansky V.A., Shirkalin
I.A., Thermodynamic equilibria and extremes:
Analysis of thermodynamic accessible regions and partial equilibria in physical, chemical, and technical systems. Springer, 2007. (Обзор
вычислительных алгоритмов термодинамического анализа и его приложений к
реальным и модельным системам.)